
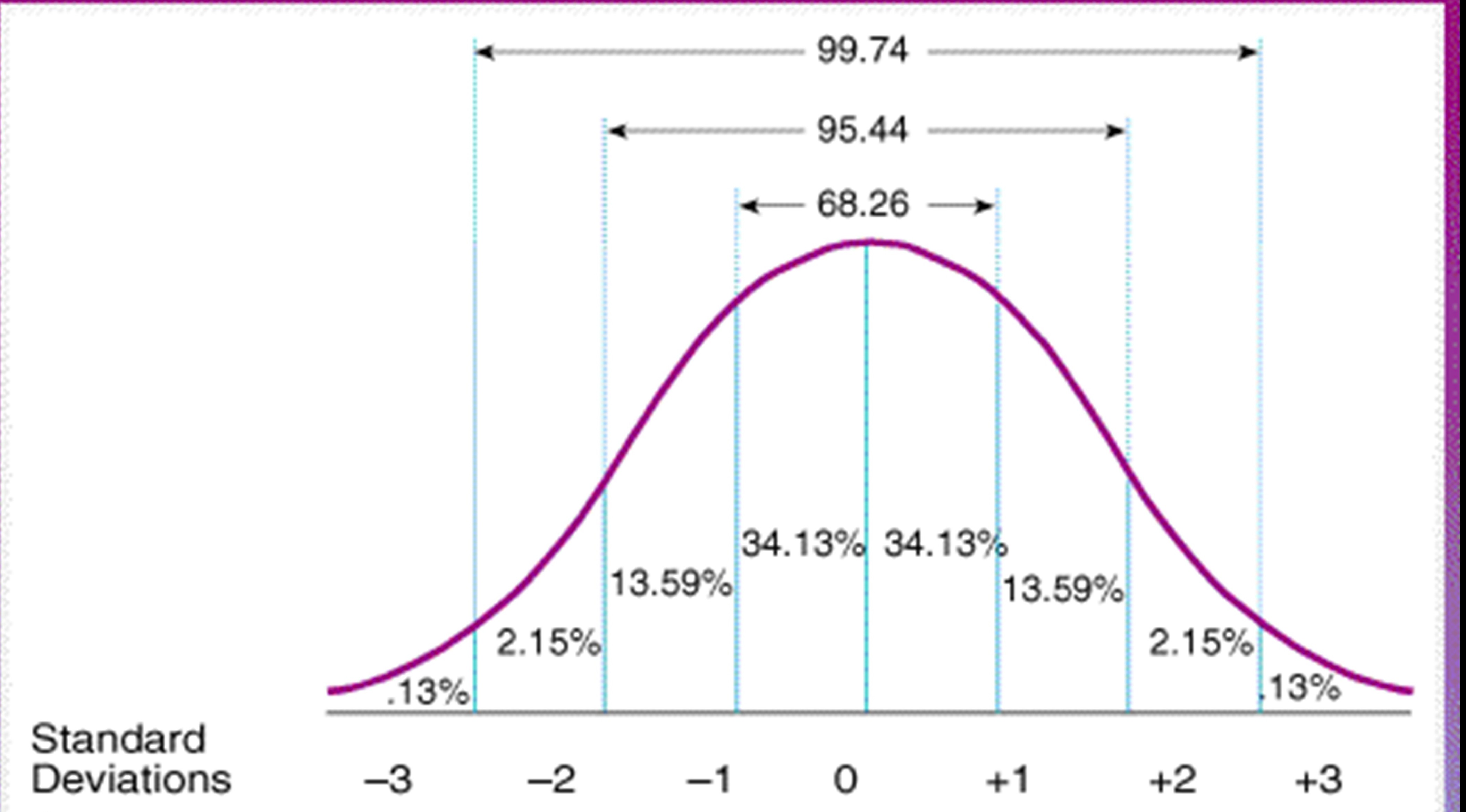
About 95 percent of the x values lie within two standard deviations of the mean.The z-scores are –1 and +1 for 44 and 56, respectively. The values 50 – 6 = 44 and 50 + 6 = 56 are within one standard deviation from the mean 50. Therefore, about 68 percent of the x values lie between –1 σ = (–1)(6) = –6 and 1 σ = (1)(6) = 6 of the mean 50. About 68 percent of the x values lie within one standard deviation of the mean.Suppose x has a normal distribution with mean 50 and standard deviation 6. The empirical rule is also known as the 68–95–99.7 rule. These facts can be checked, by looking up the mean to z area in a z-table for each positive z-score and multiplying by 2. So, in other words, this is that about 68 percent of the values lie between z-scores of –1 and 1, about 95% of the values lie between z-scores of –2 and 2, and about 99.7 percent of the values lie between z-scores of -3 and 3. The z-scores for +3 σ and –3 σ are +3 and –3, respectively.The z-scores for +2 σ and –2 σ are +2 and –2, respectively.The z-scores for +1 σ and –1 σ are +1 and –1, respectively.Notice that almost all the x values lie within three standard deviations of the mean. About 99.7 percent of the x values lie between –3 σ and +3 σ of the mean µ (within three standard deviations of the mean).About 95 percent of the x values lie between –2 σ and +2 σ of the mean µ (within two standard deviations of the mean).About 68 percent of the x values lie between –1 σ and +1 σ of the mean µ (within one standard deviation of the mean).The Empirical Rule If X is a random variable and has a normal distribution with mean µ and standard deviation σ, then the Empirical Rule states the following: This score tells you that x = 10 is _ standard deviations to the _ (right or left) of the mean_ (What is the mean?). Suppose Jerome scores 10 points in a game. Jerome averages 16 points a game with a standard deviation of four points. We can find this answer (or z-score) by writing We want to determine the number of standard deviations the score of 11 falls above the mean. Suppose we have a data set with a mean of 5 and standard deviation of 2. Adding μ to both sides of the equation gives μ + ( z ) ( σ ) = x μ + ( z ) ( σ ) = x. Multiplying both sides of the equation by σ gives: ( z ) ( σ ) = x − μ ( z ) ( σ ) = x − μ. The score itself can be found by using algebra and solving for x. The standard normal distribution allows us to interpret standardized scores and provides us with one table that we may use, in order to compute areas under the normal curve, for an infinite number of data sets, no matter what the mean or standard deviation.Ī z-score is calculated as z = x − μ σ z = x − μ σ. Z-scores can be looked up in a Z-Table of Standard Normal Distribution, in order to find the area under the standard normal curve, between a score and the mean, between two scores, or above or below a score. Likewise, it does not make sense to compare scores from two different samples that have different means and standard deviations. It would not make sense to compare apples and oranges. Z-scores allow for comparison of scores, occurring in different data sets, with different means and standard deviations. A z-score indicates the number of standard deviation a score falls above or below the mean. It represents a distribution of standardized scores, called z-scores, as opposed to raw scores (the actual data values). Pr ( μ − 1 σ ≤ X ≤ μ + 1 σ ) ≈ 68.27 % Pr ( μ − 2 σ ≤ X ≤ μ + 2 σ ) ≈ 95.45 % Pr ( μ − 3 σ ≤ X ≤ μ + 3 σ ) ≈ 99.The standardized normal distribution is a type of normal distribution, with a mean of 0 and standard deviation of 1. In mathematical notation, these facts can be expressed as follows, where Pr() is the probability function, Χ is an observation from a normally distributed random variable, μ (mu) is the mean of the distribution, and σ (sigma) is its standard deviation: In statistics, the 68–95–99.7 rule, also known as the empirical rule, is a shorthand used to remember the percentage of values that lie withinĪn interval estimate in a normal distribution: 68%, 95%, and 99.7% of the values lie within one, two, and three standard deviations of the mean, respectively. The y-axis is logarithmically scaled (but the values on it are not modified). Prediction interval (on the y-axis) given from the standard score (on the x-axis).
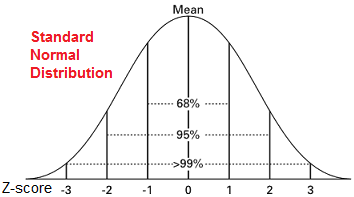
Shown percentages are rounded theoretical probabilities intended only to approximate the empirical data derived from a normal population. Shorthand used in statistics For an approximately normal data set, the values within one standard deviation of the mean account for about 68% of the set while within two standard deviations account for about 95% and within three standard deviations account for about 99.7%.


 0 kommentar(er)
0 kommentar(er)
